3A. Roman labyrinths, examples

In this section some examples of different types of Roman labyrinths will be shown, picked from the catalogue in the splendid book “Through the Labyrinth” of Hermann Kern (in English 2000, in German 1982). (If I am not permitted to bring those copies I shall withdraw this page).

Contents of figures (photos):

	from YEAR	SIZE	ENTRANCE	CIRCUL.	WAVE
Fig. ra1: Tunisie H	ca. 300	Si42-8r17	bottom	anti-clock	8 B
Fig. ra2: Salzburg	275 – 300	Si37-11r13	right	clockwise	3 C
Fig. ra3: Alger	324	Si29-7ra11	bottom	anti-clock	1 D+2
Fig. ra4: Schweiz A	ca. 250	Ci14-4r5	low left corn	anti-clock	1 C
Fig. ra5: Rome Palatine	ca. 75	Pi19-9r5	top	clockwise	2 B
Fig. ra6: Schweiz F	200 – 225	Ci26-8r9	top left	clockwise	4 B
Fig. ra7: Srbija	ca. 300	Pi19-1	no entr /exit		2 C
Fig. ra8: Kypros, photo	4	Ci25-9r8	bottom	anti-clock	1 C
Fig. ra9: Kypros, drawing
Fig. ra10: Tunisie S	200 - 250	Si46-4r21	bottom	anti-clock	special
Fig. ra11: Pompeji	80 – 60 BC	Si34-8r13	top	anti-clock	3 C
Fig. ra12: Nîmes, Troja 2	ca. 100	Si16-2tr7	top	troja 2	troja 2
Fig. ra13: Wales, photo	ca. 200	Si31-5rw13	?	clockwise	3 C
Fig. ra14: Wales, drawing 1	my drawing	Si31-5rw13
Fig. ra15: Wales, drawing 2	my drawing	Si31-5rw13
Fig. ra16: Alger, drawing 1	my drawing	Si29-7ra11
Fig. ra17: roma-alger labyrinths, quadrant 2 – 4	my drawing
Fig. ra18: roma-alger labyrinths, quadrant 1	my drawing

Roman labyrinths are mosaic floor labyrinths from villas and baths in the Roman Empire and many of them are square, and they are too small to be walked, (with exceptions). We shall here include also non-square forms.

In section 3 of this website the Roma-Piadena Labyrinth is analysed. It is a beautiful labyrinth and a smart type in its “turning of direction” in the 4’ quadrant to reach the goal in the centre. 4 examples of this type have been found (Piadena, Cremona, and 2 in Pompeii). In most other Roman labyrinths reaching the centre is obtained simple by adding an extra quadrant lane or radial lane adjacent to the entrance quadrant lane:

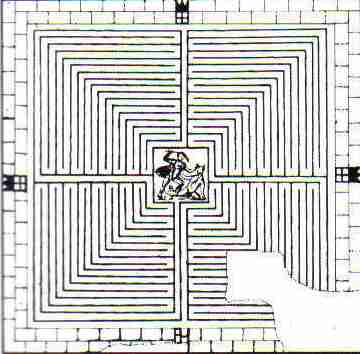
Fig. ra1: Tunisie H

Tunisia, Henchir el Faouar, dating ca. 300. Labyrinth mosaic floor is still in situ.

Si42-8r17, entrance: bottom, anti-clockwise, 8 waves B in-out, double quadrant lane entrance + goal out-in.

In this labyrinth each quadrant consists of many waves of wave form B, of 8 simple waves of 2 lanes. (Contrary to this: the Alger Labyrinth with 1 wave of many lanes, fig. ra3).

Entrance lane and the final goal lane are in the bottom of the drawing, and it is distinct that at the entrance quadrant there are 2 adjacent lanes and only 1 lane in the other 3 quadrants. Each quadrant starts at the centre and ends at the perimeter so to reach the centre goal an extra final radial quadrant lane is simply added, the usual system in roman labyrinths.

It is a big labyrinth of simple layout easy to comprehend. (A small cross line blocking the path at the top of the drawing should be disregarded).

Explanation: The labyrinth is Square with internal goal, 42 lanes in area or in cross section, 8 lanes centre area, roman, 17 lanes or 17 turns in each quadrant. Entrance is at the bottom of this drawing with upright centre figure (of Theseus killing the Minotauros), quadrant 1 is to the right of the entrance and then the labyrinth walker proceeds anti-clockwise to the next quadrant. The basic wave figure is B moving from the centre and out to the perimeter. To reach the goal in the centre a final extra lane is placed adjacent to the entrance lane taking the needed space from either quadrant 1 or 4 (or both).

Fig. ra2: Salzburg

Austria, now Vienna Art Museum, originated near Salzburg, dating 275 – 300.

Si37-11r13, entrance: right, clockwise, 3 waves C in-out, double quadrant lane entrance + goal out-in.

The black lines are the walls, the red lines are the lanes = the path to be walked (= the Ariadne thread).

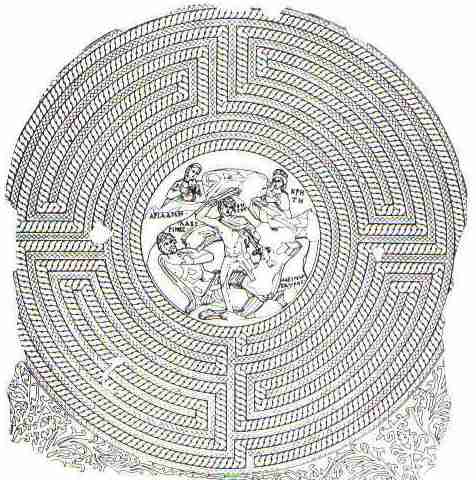
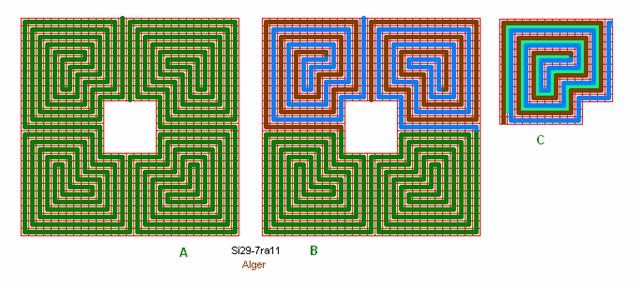
Fig. ra3: Alger

Algeria, Cathedral of Algiers, originated from the Basilica in Al Asnam founded 324.

Si29-7ra11, entrance: bottom, anti-clockwise, 1 wave D+2 in-out, double quadrant lane entrance + goal out-in.

The wave figure is D with the tip of the tong having further 2 turns as a spiral. (Contrary to this is the Tunisie H Labyrinth with many waves of 2 lanes, fig. ra1). This is the first Roman labyrinth to convey a Christian meaning (Kern says). The centre is a holy text written in a “labyrinthine manner”.

A system of Roma-Alger labyrinths are shown below in fig. ra16 - ra18.

Fig. ra4: Schweiz A

Switzerland, Avenches, dating ca. 250.

Ci14-4r5, entrance: lower left corner, anti-clockwise, 1 wave C in-out, double quadrant radial lane entrance + goal out-in.

The centre picture shows (only) the horn of the Minotauros and Theseus’ dagger.

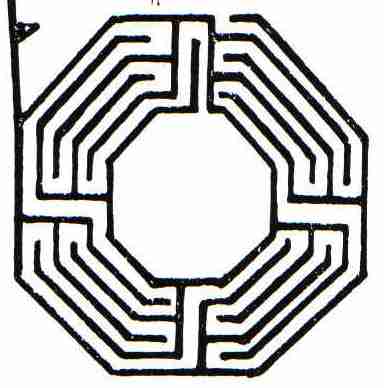
Fig. ra5: Rome Palatine

Italy, Imperial Palace on the Palatine, dating ca. 75.

Pi19-9r5, entrance: top, clockwise, 2 waves B out-in, double final quadrant lane to goal in-out + out-in.

The 8 sided polygon labyrinth is 20 meters in width giving 1 meter wide lanes to be walked to get to a fountain in the centre.

Fig. ra6: Schweiz F

Switzerland, Fribourg, dating 200 – 225.

Ci26-8r9, entrance: top left, clockwise, 4 waves B in-out in 8 sections, double radial lane entrance + goal out-in.

Fig. ra7: Srbija

Serbia, Gamzigrad, dating ca. 300.

Pi19-1, no entrance and no exit to goal, anti-clockwise if radial lane out-in, 2 waves C then in-out.

6 sided polygon with 3 sections.

Fig. ra8: Kypros, photo

Cyprus, Kato Paphos, dating year 4.

Drawing in the next figure, fig. ra9.

Ci25-9r8, entrance: bottom, anti-clockwise, 1 spiral + 1 wave C + 1 spiral out-in, only 3 radial quadrant lanes with no quadrant lane at the entrance side.

The lane to walk is with a twisted Ariadne thread.

Fig. ra9: Kypros, drawing

See fig. ra8 above with photo and text.

Fig. ra10: Tunisie S

Tunisia, Sousse, dating 200 - 250

Si46-4r21, entrance: bottom, anti-clockwise, special wave figure: 2 B wave groups in-out of each 2 waves C out-in, double quadrant lane entrance + goal out-in.

A more advanced roman labyrinth.

Fig. ra11: Pompeji

Italy, Pompeii, 80 – 60 BC

Si34-8r13, entrance: top, anti-clockwise, 3 waves C in-out, Piadena-model: quadrant 4 has turn of direction.

Fig. ra12: Nîmes, Troja 2

France, Nîmes, dating ca. 100.

Si16-2tr7, entrance: top, a troja 2 labyrinth modified to be square (modified more than slightly, compare to fig. tr8).

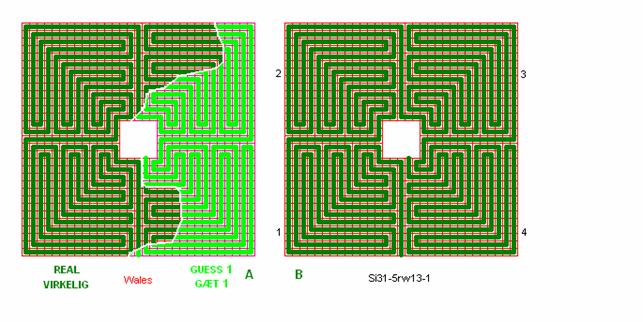
Fig. ra13: Wales, photo

Wales, Caerleon on Usk, dating ca. 200.

Si31-5rw13, entrance?, clockwise, 3 waves C (in upper left quadrant), lower left quadrant is different.

This labyrinth has lost much of the 2 quadrants to the right. I have given 2 probable solutions to the missing part below in fig. ra14 and fig. ra15 (more solutions are possible).

The upper left quadrant is a usual roman labyrinth. The lower left quadrant is different - interesting different. Many experts on labyrinths will probably say that this quadrant has a mistake and should have the same design as the upper quadrant. But the quadrant is all right to walk – interesting to walk.

Fig. ra14: Wales, drawing 1

Guess on entrance and on quadrants to the right side, guess 1:

Entrance is at the bottom, quadrant 1 is “special”, quadrant 2 is “normal”, quadrant 3 fits with being = to quadrant 2. Quadrant 4 has to be special and here the “direction is turned” to reach the goal in the centre like in the Roma-Piadena labyrinth. Quadrant 4 “points” towards quadrant 3 with the same type of narrow, normal, and wide “tongs” as quadrant 1 point towards quadrant 4.

So the Romans had a smart mosaic labyrinth designer in Wales 1800 years ago.

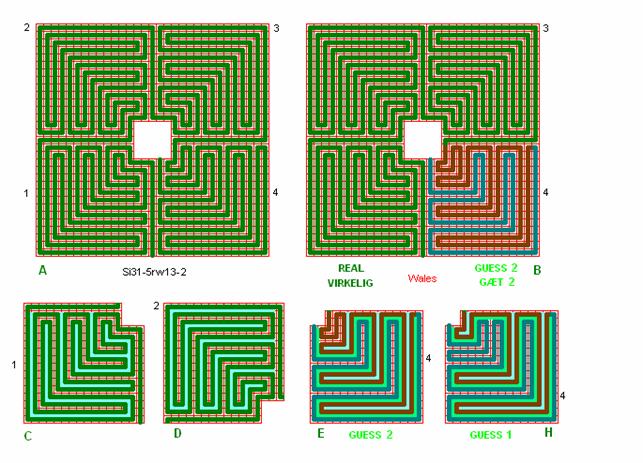
Fig. ra15: Wales, drawing 2

Guess on entrance and on quadrants to the right side, guess 2:

Compared to fig. ra14 above I have here made a slight change in the centre part of quadrant 4.

In details C, D, E, and H the wave pattern is illustrated. Turning quadrant 2 in detail D 90° clockwise it is seen that the wave pattern is wave symbol C in fig. r1. Quadrant 1 in detail C is mirrored vertically. There is 1 C-wave + 1 B-wave + 1 C-wave with an extra “back splashing” tong. In quadrant 4 in detail E we see a “snake wave” waving as wave B like in wave symbol H in fig. r1, with a slight variation so it is a wave symbol K. In guess 1 (from fig. ra14 above) it is a different wave symbol K.

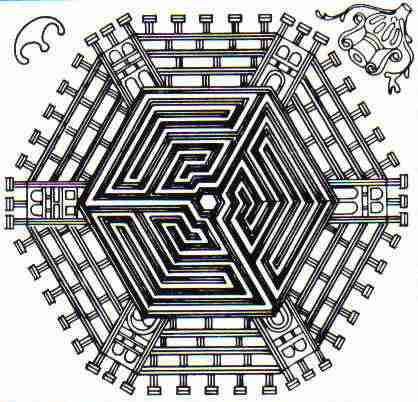
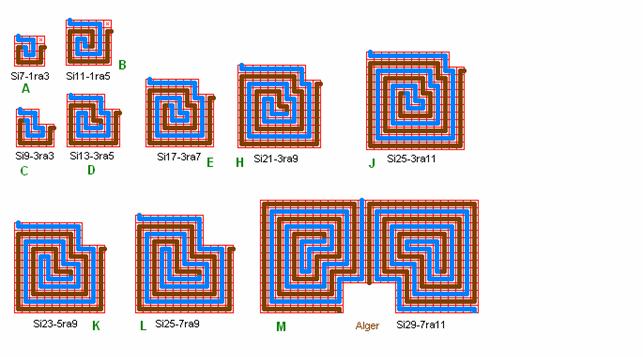
Fig. ra16: Alger, drawing 1

Algeria, Cathedral of Algiers, from fig. ra3. The labyrinth is here turned 180°, to comply with the other roma labyrinths in section 4 of this website. The needed area for the extra quadrant lane at the end to get to the goal in the centre is obtained by squeezing quadrant 1 with the entrance lane. In detail C there is shown the wave figure of all 4 quadrants, and in wave symbol D of fig. r1 the tong needs to continue in another 2 turns, so we have 1 wave D+2 in each quadrant. A system of roma-alger labyrinths can be made with just 1 wave in each quadrant, as shown in fig. ra17 – ra18 below.

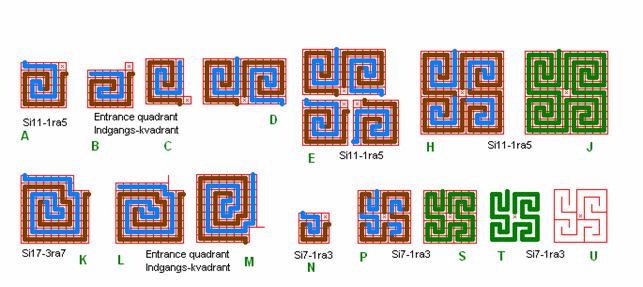
Fig. ra17: roma-alger labyrinths, quadrant 2 – 4

Fig. ra18: roma-alger labyrinths, quadrant 1

By squeezing quadrant 2 in detail A it is shown how to get quadrant 1, the entrance quadrant, in detail C, to make the whole labyrinth Si11-1ra5 in detail J.

Likewise the entrance quadrant in M is made from quadrant 2 in K.

The smallest roma-alger labyrinth is Si7-1ra3 in detail S.

To summary

To section 4 roma labyrinths