5. Chartres Chartres
The
labyrinth in the Chartres Cathedral from about year 1200 is a circular labyrinth
of flagstones in the floor. It is big and the lane pattern seems at the first
view to be easy comprehensible and simple but it shows to be complicated and
unpredictable as it is said in the book ”Alle tiders labyrinter”of Jørgen
Thordrup, 2002. I have here drawn this 11 circle lane big labyrinth in the more
flagstone adapted square form and this makes it even more difficult to grasp
quickly.
But if the
lane pattern is “straightened out” to a rectangular formed system figure as
shown in the following figure in detail C the lane pattern will be ready for a
more easy analysis.
Below I
have shown in fig. C4 how
the Chartres Labyrinth consists of a rather simple elementary figure and by
which a number of bigger chartres labyrinths can be designed.
Symbols and units:
See the section on labyrinths in roma style.
Contents for figures:
Fig. C1: The Chartres Labyrinth and
its system
Fig. C3: Succession in 4 sections
Fig. C4: Chartres made of the
elementary figure ch5
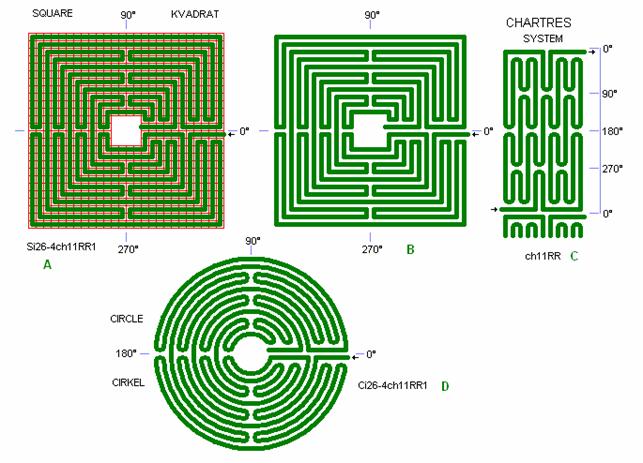
Fig. C1: The Chartres Labyrinth and its system
The
Chartres Labyrinth in Chartres is here drawn in square form and circular form
and shown in a system figure in detail C. See photo in fig. i4 in
section 1. There is used the same line stroke and lane width as for other
drawings of chartres and roma labyrinths on this website. (The labyrinth in the
Chartres cathedral has more narrow intervals between the lanes which gives more
beautiful tips of tongs). The Chartres Labyrinth is 11 lanes wide from the
centre space to the outer edge. It consists of “tongs” that are 90° and 180°
long, and of 2 radial line lanes at 0° from the outer edge to the centre space
edge. In the quadrant lines 90°, 180°, and 270° there is a beautiful symmetry
with alternately tong and line. By the 2 radial lines at 0° the symmetry is
dislocated by one lane, so here the interesting experience is: “first look to
the left, then look to the right” when walking the left radial lane as the
start of the labyrinth and again when walking the right radial lane to finish
the labyrinth.
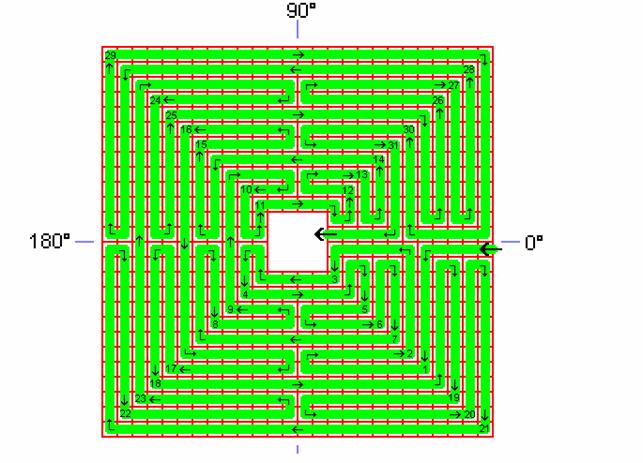
Fig. C2: Lane walking
The
Chartres Labyrinth as square with the specification of the lane succession.
This is
better seen on the following system figure:
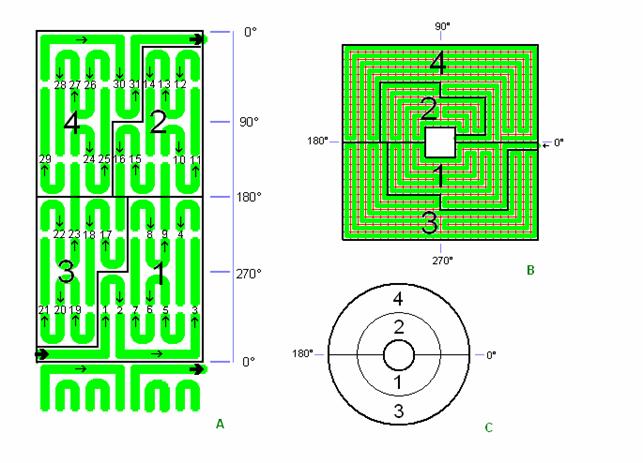
Fig. C3: Succession in 4 sections
The Chartres
Labyrinth is walked, is traversed after turn in 4 sections.
Right from
the start at the outer edge you walk straight towards the centre along a radial
lane (like in the roma labyrinth) and after a small trip out into a 90° tong
halfway you walk right up to the edge of the centre space. The labyrinth is
then walked after turn in 4 sections of 180° as shown approximately on the
circle in detail C and shown precisely in detail A and B. First the 2 inner
areas are walked and then the 2 bigger outer areas, and at the end you are led
from the outer edge lane directly to the goal in centre, except again for a
small walk out into a 90° tong. (This long walk can in the Chartres Cathedral
have been a pilgrim walk on your knees to the special holy centre area).
You can
maybe see the
The
Chartres Labyrinth is unsurpassed interesting and beautiful with its tong
symmetries at the quadrant lines 90°, 180°, and 270°. Maybe the symmetry at 0°
will be questioned then with the 2 radial lanes here. These 2 radial lanes do
both need halfway to have a small turn out into a solitude tong for the
completeness of the labyrinth (see fig. C4), but this is probably only an extra
interesting feature to this beautiful classic labyrinth.
The
Chartres Labyrinth is the basis for a whole system of
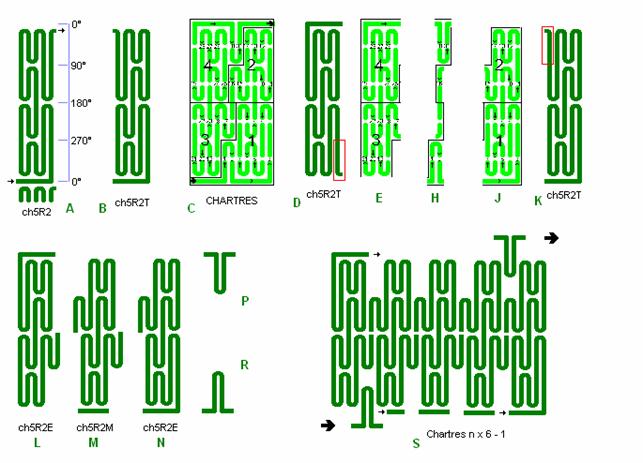
Fig. C4: Chartres made of the elementary figure
ch5
In section
6 with labyrinths of
ch5R2 in
detail A has it upper half twisted to ch5R2T in B. In C we have the Chartres
lane pattern from fig. C3 above, which is divided into 3 parts E, H and J. By
this it is seen that the Chartres Labyrinth is made of ch5R2T changed to ch5R2E
in L and N together with 2 solitude tongs on the radial lanes as in P and R.
From ch5R2T
we also get the internal part ch5R2M shown in detail M. By this a variable big
chartres labyrinth can be made of the 2 “end pieces” L and N + some “internal
pieces” M, e.g. as shown in S: a chartres 29 with 3 internal pieces so that n =
5. In all “intervals” a radial lane tong P and R must then be inserted, here a
total of 4 on the start lane + 4 on the finish lane. Like the real Chartres
Labyrinth this labyrinth has the beautiful symmetry with alternately tong line
tong line in the quadrant lines 90°, 180°, 270°.
The real
Chartres Labyrinth consists of only the 2 end pieces L and N without any
internal piece, i.e. n = 2 which gives 2 x 6 - 1 = ch11.
Contents of the other
sections:
6 Labyrinths
of chartres style
7 Comparing
labyrinth-examples