6. Labyrinths of chartres
The most
characteristic about the Chartres Labyrinth in
A labyrinth
of the chartres style should comply with the
following rules
- it has narrow tongs 90° and
180° long
- there is symmetry in the
quadrant lines 90°, 180°, and 270°
- there are 2, 1, or 0 radial
lanes in 0° and only here
Square and circular
The
labyrinth can be circular, square, or rectangular or of other forms. The size
of the area in the centre is according to need.
We will
here consider some examples of labyrinths of the chartres
style. They will be smaller than the big true Chartres Labyrint in
The figures
are orientated with 0° and 90° as in mathematics, and walking the lane from
outside begins with the part of the labyrinth on the left hand.
Symbols and units:
See the section on labyrinths in roma
style.
Contents for figures:
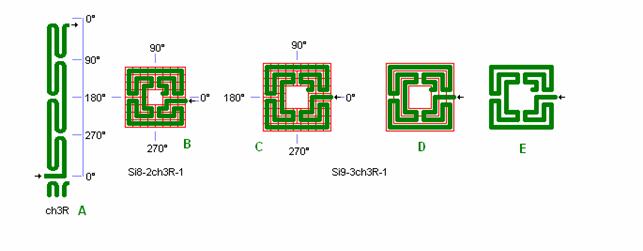
Fig. ch2: ch3 system in Si8-2 and Si9-3
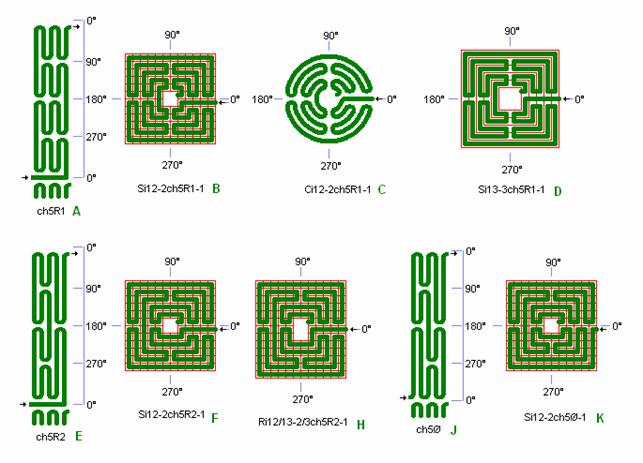
Fig. ch3: ch5R1, ch5R2, and ch5Ø in Si12-2 and Ci12-2 etc.
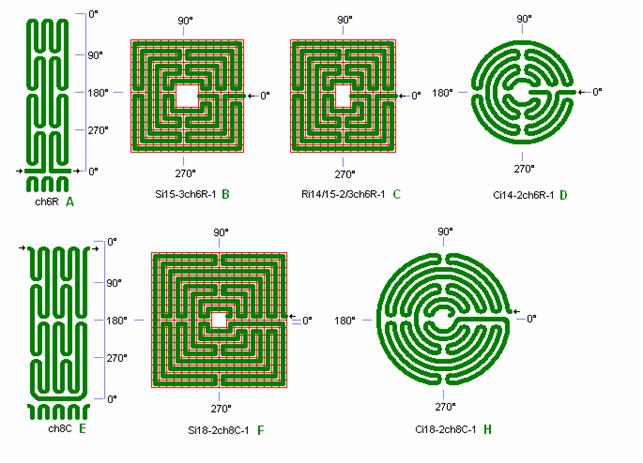
Fig. ch4: ch6R and ch8C in e.g. Si15-3, Ci14-2, Si18-2, Ci18-2
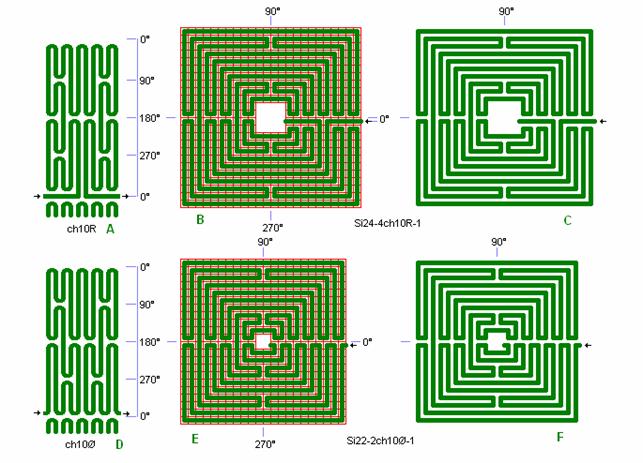
Fig. ch5: ch10R and ch10Ø in Si24-4 and Si22-2
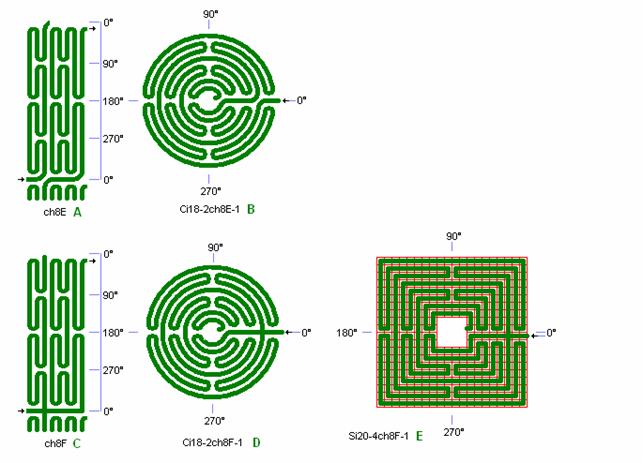
Fig. ch6: ch8E and ch8F in Ci18-2, Ci18-2, and Si20-4
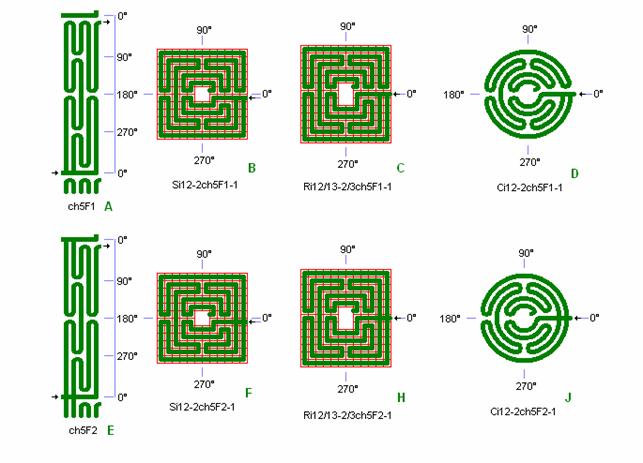
Fig. ch7: ch5F as multiple choice labyrinth
in Si12-2 and Ci12-2
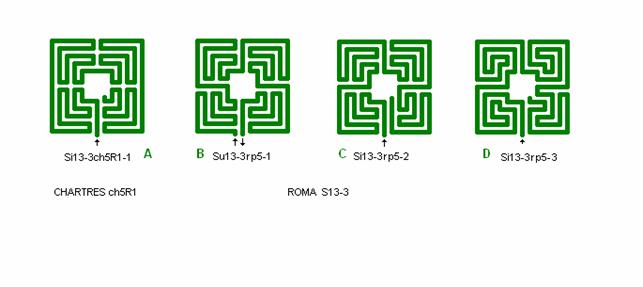
Fig. ch8: Comparison between chartres
ch5R1 and roma S13-3
Fig. ch1: Chartres
systems
We here see
some proposals for labyrinths according to the chartres
principle. These labyrinths are all smaller than the original
labyrinth in Chartres (which is ch11).
For the
clearness the labyrinths are here shown in rectangular symbolic form.
Labyrinths bigger than the original Chartres are
obtained by combination and extension. See also the extended
ch3R is the smallest labyrinth. It is 3 lanes wide,
and has 1 radial lane from the edge to the centre area.
ch5R is an extension of ch3. With an additional 90°
tong in each quadrant as shown we get ch5R1, or with 2 tongs 180° we get ch5R2.
With additional extension with 90° tongs and 180° tongs we can get ch7R systems
and ch9R systems etc. which is not shown here.
ch6R is made by combining ch3R and mirrored ch3R.
ch8R is made by combining ch3R and mirrored ch5R2.
ch9R is made by combining ch6R and mirrored ch3R.
ch10R is made by combining ch5R2 and mirrored ch5R2.
ch8C is made by combining mirrored ch3R and ch5R2.
Radial lane can have a sharp bend.
ch10C is made by combining mirrored ch5R2 and ch5R2.
ch8E is made by combining ch3R and
ch5R2.
ch10E is made by combining ch5R2 and
ch5R2.
ch5Ø is made from ch5R2 by mirroring the
lower 180° part and erasing the radial lane.
ch10Ø is made by combining ch5Ø and mirrored ch5Ø.
The shown ch-systems can be bent to give circular labyrinths or
square labyrinths or labyrinths of other forms.
ch8E and
ch10E can give a circular labyrinth but not a square labyrinth because of an
overlap in the radial lane crossing.
The 360°
circle is here divided into 4 to 90°, 180°, 270°. There can also be divided
into e.g. 3 to 120° and 240° etc.
Fig. ch2: ch3 system in Si8-2 and Si9-3
ch3 shown
as square labyrinth, the smallest chartres labyrinth.
In detail B
the smallest unit is a check pattern of 1. This does not give perfect symmetry
of tongs by 0° quadrant line. In detail C, D, and E there is perfect tong
symmetry by changing the centre square from 2 x 2 to 3 x 3 and by using a unit
of ½ where the tongs meet at 90°, 180° and 270°.
With a
check = 1 x 1 m the lane width = 1 m total and the Si8-2 labyrinth square = 8 x
8 m with 2 x 2 m centre square as the goal.
Fig. ch3: ch5R1, ch5R2, and ch5Ø in Si12-2 and
Ci12-2 etc.
ch5 to
square, and rectangle, and circle.
In detail D
there is complete tong symmetry for ch5R1 using ½ check unit as for ch3 above
in fig. ch2.
In detail H
ch5R2 is shown in rectangular form so the radial lane is in the middle of the
entrance side. All the chartres labyrinths can in
this easy way be stretched to rectangular form. (This can be difficult for some
roma labyrinths).
ch5R1 in
detail A, B, C, and D walks the 4 quadrants in turn, in partly the same way as
for a roma labyrinth. But the roma
should have 4 radial lanes instead of just 1. See the comparison with roma below in fig. ch8.
ch5R2 is
perhaps more of chartres style than ch5R1 by moving
more over 180° with alternately tongs and lines in the quadrant lines. There is symmetry
of tongs in all 4 quadrant lines and symmetry between 90° and 270°.
Ch5Ø in detail K is without radial lane in 0°. By this the full symmetry by
0° is lost.
Fig. ch4: ch6R and ch8C in e.g. Si15-3, Ci14-2,
Si18-2, Ci18-2
Fig. ch5: ch10R and ch10Ø in Si24-4 and Si22-2
In 90° and
270° there are only 2 tongs and many lines. ch10Ø is without radial lane in 0°
and here the many tongs meet without symmetry.
Fig. ch6: ch8E and ch8F in Ci18-2, Ci18-2, and
Si20-4
ch8E cannot
be used as a square labyrinth because of 2 lanes crossing the same check (same
flagstone). If this point is changed to make it a multiple choice labyrinth as
shown in ch8F, which gives full symmetry in 0°, then ch8 can also be used as
square as shown in detail E.
Fig. ch7: ch5F as multiple choice labyrinth in
Si12-2 and Ci12-2
If you in
the radial lane in ch5F1 choose to go left into lane no. 2 or into the inner
lane then you just end at start again. The edge lane furthest from the centre
is the right way to the centre.
ch5F2 is
more symmetrical than chF1 and it is good for a special game for children (or
for young people in love): “You cannot catch me!” In ch5F2 right after start
there are 5 choices. The 2’ lane to the right leads to the centre, and you are
caught if someone pursues you. Try this game with your 3 year old grandchild.
This labyrinth in detail F is used for the outer multiple choice
Fig. ch8: Comparison between chartres ch5R1 and roma S13-3.
Roma
traverses each quadrant completely after turn. So does this Chartres
ch5R1 though directed outwards inwards
outwards inwards. Chartres
has only 1 radial lane, while roma has 4 radial
lanes, one in each quadrant line.
Roma in
detail B has both entrance and exit at the edge. In C this is changed to have
goal in the centre by just leading the exit at the edge to the centre by still
another radial lane, so that there are 2 radial lanes by the entrance. This
principle is seen in some classical Roman type labyrinths. Then I find the roma labyrinth in D more according to the Roma-Piadena principle, see detail A
with roma basics in fig.
r2.
Contents of the other
sections:
5 Chartres Labyrinth in Chartres
7 Comparing
labyrinth-examples